Skip to main content
Your accuracy score measures how close your prediction is to the realized outcome. Every prediction on Trepa gets an accuracy score between 0 and 1 after the result is known.
  • Scores closer to 1 mean you were very close.
  • Scores closer to 0 mean you were far from the result.
Trepa runs score-weighted, time-adjusted, ROI-capped pari-mutuel pools that redistribute capital from less accurate predictors (“losers”) to more accurate ones (“winners”). The accuracy score is the “score-weighted” part of that design.

​
How accuracy is calculated

When a pool resolves, Trepa computes your accuracy score in three main steps.

​
1. Measuring errors

Trepa first measures your absolute error, the distance between your prediction and the outcome. absolute error=∣prediction−outcome∣\text{absolute error} = \lvert \text{prediction} - \text{outcome} \rvert Smaller error means you were closer to the truth.

​
2. Finding the stake-weighted median error

Next, Trepa looks at the errors of everyone in the pool and finds the weighted median prediction error.
  1. It sorts all participants by their error from smallest to largest.
  2. It tracks how much cumulative stake sits at each error level.
  3. It finds the error where half of the total stake lies on each side.
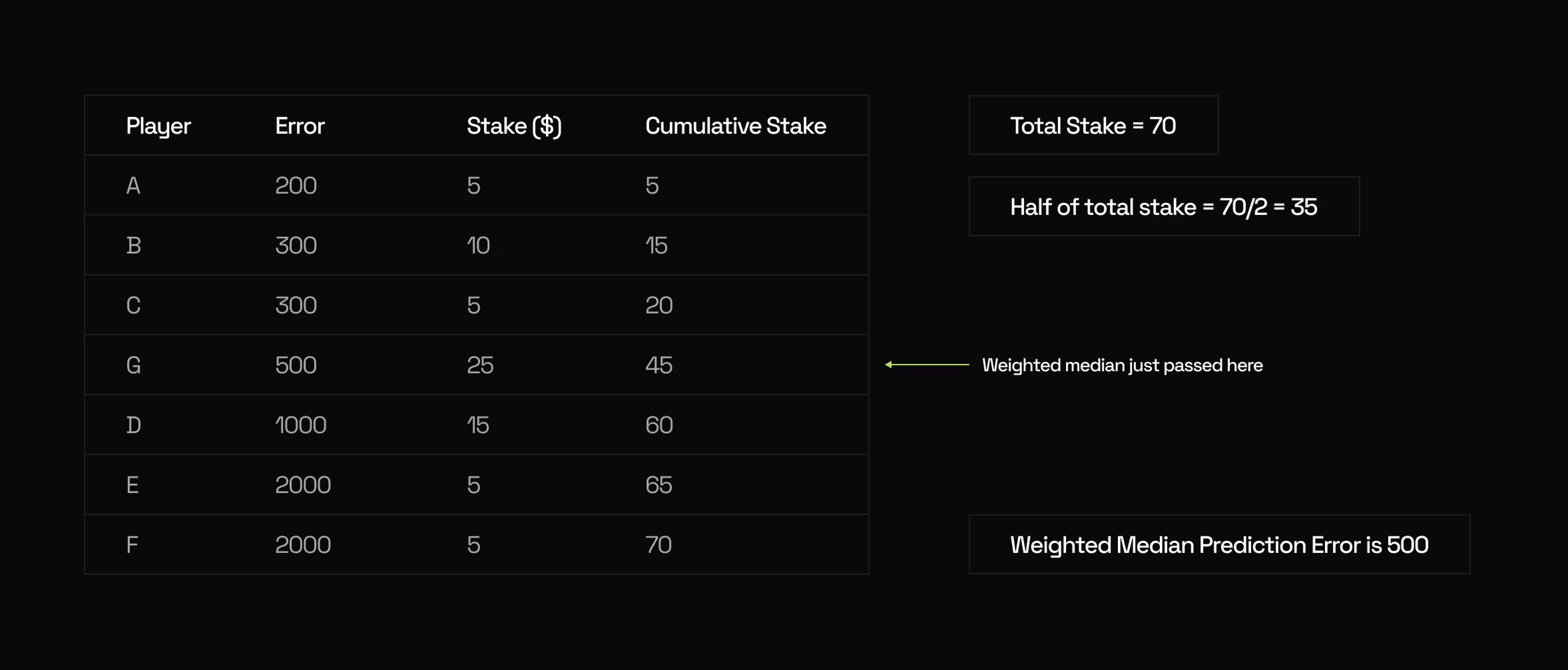
image.png
The weighted median baseline is invariant under splitting a stake into many mini stakes with the same prediction. Sybil leverage is thus limited to total stake mass, not account count.

​
3. Normalize your error and map it to a score

Trepa then normalizes your error relative to the median error. normalized error=your errormedian error\text{normalized error} = \frac{\text{your error}}{\text{median error}}
  • A normalized error below 1 means you were closer than the typical participant.
  • A normalized error above 1 means you were further away than the typical participant.
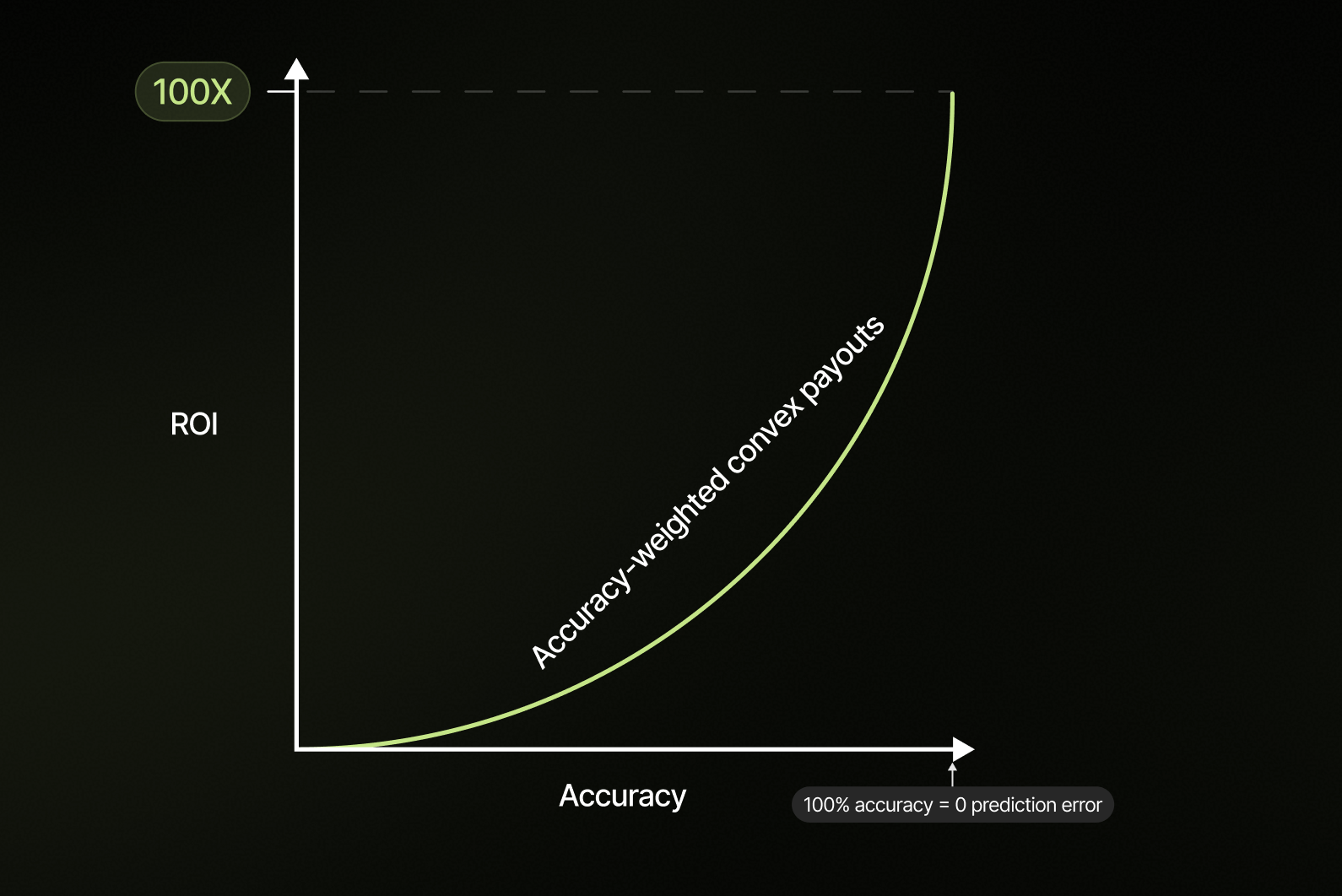
Finally, Trepa feeds this normalized error into a convex, strictly decreasing accuracy function. accuracy score=(11+normalized error)γ,γ>0.\text{accuracy score} = \left(\frac{1}{1 + \text{normalized error}}\right)^{\gamma}, \quad \gamma > 0. This ensures smooth payout curves that emphasize precision at the top (“jackpot” structure for most accurate participants). Convex Graph
  • A normalized error of 0 (perfect prediction) gets an accuracy score of 1.
  • As normalized error increases, the score smoothly decreases toward 0.
  • Because the curve is convex, small improvements when you are already close to the outcome can increase your score a lot.